Etiqueta: Computational Imaging
-

Easy Ghost Imaging simulations (and some codes to do it at home)
A few weeks ago I gave a short seminar on how to do very simple Ghost Imaging simulations. So simple that you can run then in your latptop in a few seconds (or minutes), and you can use them as building blocks to develop larger projects. I created a Github repo with all the codes…
-
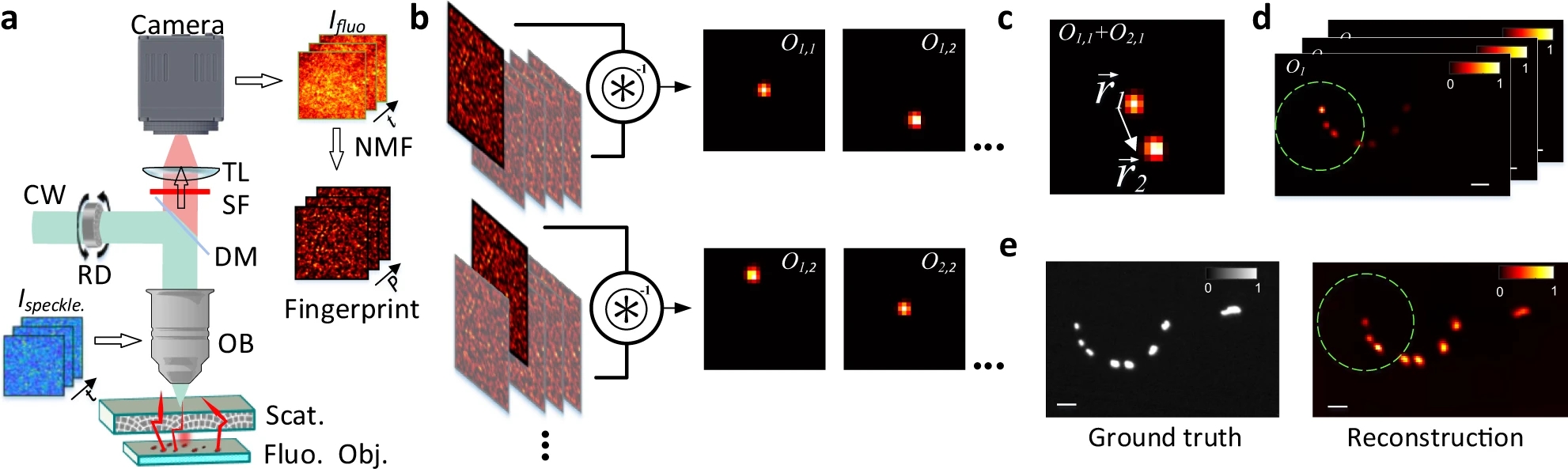
Large field-of-view non-invasive imaging through scattering layers using fluctuating random illumination
During my stay in Paris, one of the topics I have been working on is related to the problem of imaging objects hidden by scattering media. While seeing stuff through transparent materials is quite easy, the thing becomes much more complicated when light gets randomly deviated in all directions. This might seem quite a particular…
-

AI regulation, 3D displays, and more: THE WEEKLY RECAP (2022#19)
Summer is here! Temperatures on the rise (we almost reached 30ºC for a couple days), and rain seems to be over (not saying that too loud, I do not want to jinx it). Lots of interesting news this week, so let’s get to it. A dinner with Myxomycetes Really nice macro photographies of slime moulds.…
-

Maus, the Pixel experience, and more: THE WEEKLY RECAP (2022#04)
I. Need. To. Sleep. Week. Has. Been. Ex. Haus. Ting. Fox only, no items, final destination A couple cool pieces on how mainstream video games have become. The one on FT goes along the huge amounts of money the industry has been generating during the last decades, overcoming other forms of cultural content such as…
-
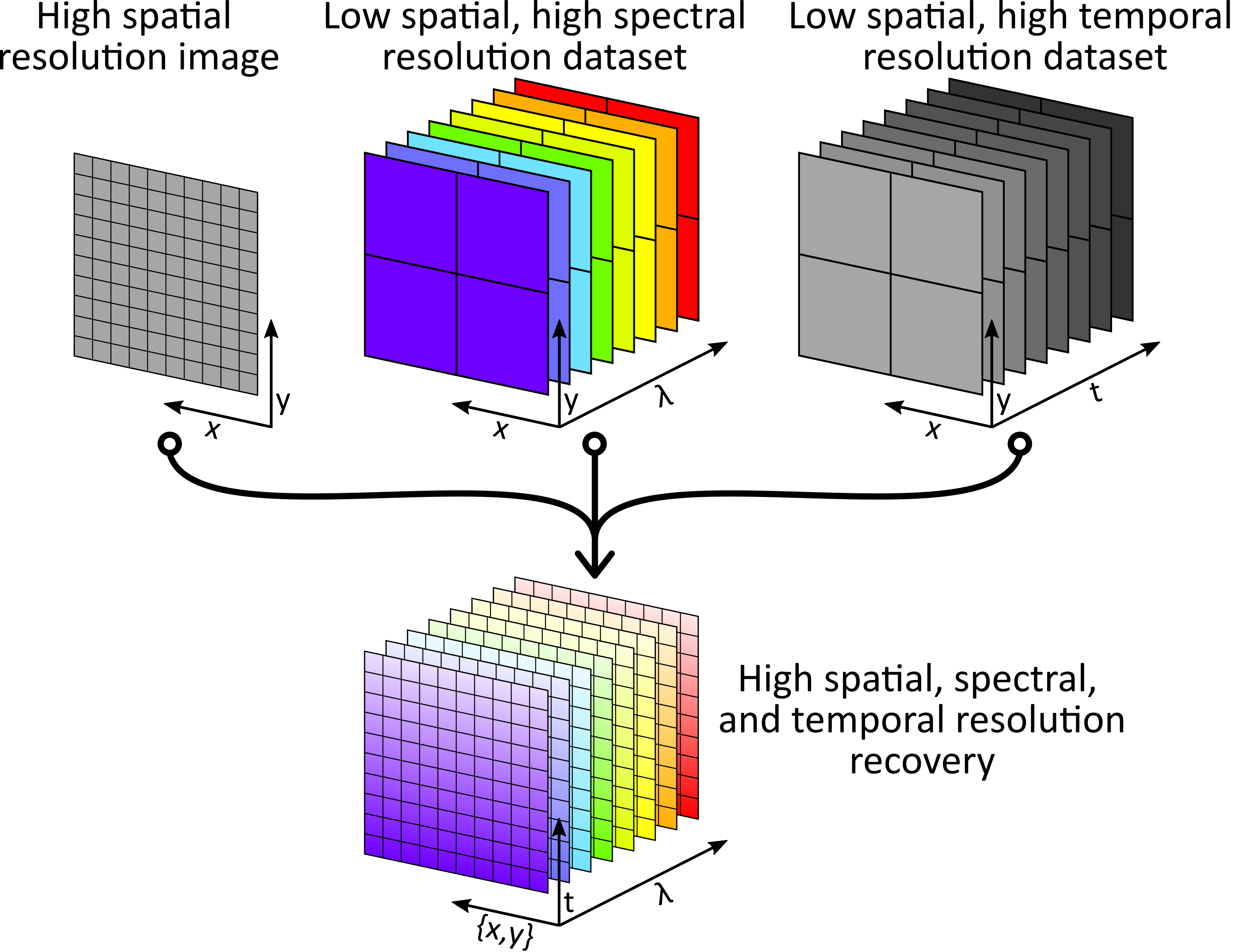
Giga-voxel multidimensional fluorescence imaging combining single-pixel detection and data fusion
Some time ago I wrote a short post about using Data Fusion (DF) to perform some kind of Compressive Sensing (CS). We came with that idea when tackling a common problem in multidimensional imaging systems: the more you want to measure, the harder it gets. It is not only the fact that you need a…
-
Data fusion as a way to perform compressive sensing
Some time ago I started working on some kind of data fusion problem where we have access to several imaging systems working in parallel, each one gathering a different multidimensional dataset with mixed spectral, temporal, and/or spatial resolutions. The idea is to perform 4D imaging at high spectral, temporal, and spatial resolutions using some single-pixel/multi-pixel…
-
Inverse Scattering via Transmission Matrices: Broadband Illumination and Fast Phase Retrieval Algorithms
Interesting paper by people at Rice and Northwestern universities about different phase retrieval algorithms for measuring transmission matrices without using interferometric techniques. The thing with interferometers is that they provide you lots of cool stuff (high sensibility, phase information, etc.), but also involve quite a lot of technical problems that you do not want to…
-
Single-pixel imaging with sampling distributed over simplex vertices
Last week I posted a recently uploaded paper on using positive-only patterns in a single-pixel imaging system. Today I just found another implementation looking for the same objective. This time the authors (from University of Warsaw, leaded by Rafał Kotyński) introduce the idea of simplexes, or how any point in some N-dimensional space can be…